In short:
Standard deviation is the spread of the values in a data set and indicates how much an individual value may vary from the mean. Applied to investing, standard deviation would tell an investor how much a certain stock or portfolio of stocks could vary from the trendline average price.
This may help the investor quantify the price risk associated with the stock or portfolio aiding in their calculation of the minimum required rate of return.
Key Points
- Standard deviation is the dispersion of values in a data set measure in the same units.
- In finance, standard deviation is a measure of the volatility of an asset.
- Standard deviation cannot be negative.
- The difference between standard deviation and variance is the squared value of the standard deviation, meaning the value and units of variance are not matched to the data set.
In-depth:
What is Standard Deviation
When you a bunch of data points that you are trying to interpret it is often useful to know how much these data points spread out from the average. This is where you can either calculate the variance or the standard deviation, where often, variance is calculated in the way to calculating the standard deviation.
Likely, you’ll choose to use standard deviation over variance since it will have the same units as your data points and variance will be squared, ex. “dollars” vs “dollars2”.
In investing, the standard deviation is a measure of volatility and price risk. This is because standard deviation is the measurement of how much an individual return or price point may be away from the trendline average return or price level.
If the standard deviation is high this means the asset is “riskier” since its returns or price experience more volatility or “swings”. Conversely, if the standard deviation is low this means the assets are “less risky” since their returns are grouped much closer to the trendline average.
Depending on the investment strategy of the investor, they may want to focus on stocks or assets with a large amount of volatility to trade and profit from the price movements. Other investors may add a high standard deviation stock or asset to their portfolio because it actually reduces the standard deviation of the portfolio overall -an idea of modern portfolio theory. Still, others will choose a low standard deviation stock or asset because they prefer not to have the volatility.
What may be important to note for an investor though is that “risk” is simply the possibility that a stock or asset performs differently than expected -which can be both better than expected or worse than expected.
Additionally, price is just one thing to consider in the examination of risk. For example, a company that produces commercial aircraft is inherently riskier than a company that produces cars. This is for many reasons which we discuss in our investing basics course.
Calculating Standard Deviation – Example
Although the name “standard deviation” may sound complex at first, the calculation is actually quite simple. You will subtract each data point from the average of the data points then square that number. Summing all these values together you will divide by the total number of data points minus 1. Finally, you will take the square root of the result.
This calculation will give you the standard deviation for a sample of a population. We have included the formula below.
Formula:
Population standard deviation
To understand how to apply the standard deviation formula we can look at an example calculation in a scenario.
Let’s say we’re looking at company AAPLS’s stock performance over the last 10 years. When go out and collect the annual returns for each year our data set is as follows.
Step 1:
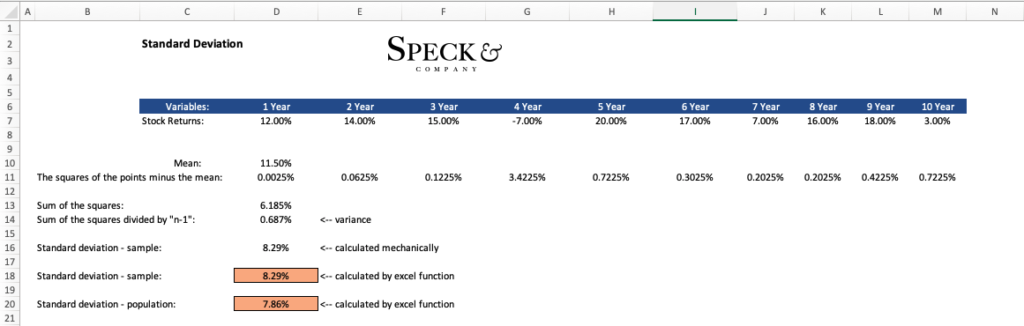
AAPLS: (year 1, 12%), (year 2, 14%), (year 3, 15%), (year 4, -7%), (year 5, 20%), (year 6, 17%), (year 7, 7%), (year 8, 16%), (year 9, 18%), (year 10, 3%)
Step 2: Now that we have the data, we need to calculate the mean by summing the returns then dividing by 10.
12%+14%+15%+-7%+20%+17%+7%+16%+18%+3% / (10) = 11.50%
Step 3: we need to subtract each value from the mean and square the result.
(12% – 11.50%)2 + (14% – 11.50%)2 + … + (3% – 11.50%)2 = 6.185%
Step 4: finally, we take the value we just calculated and divide by the number of values in our data set minus 1 since we’re using a sample.
6.185% / (10 – 1) = .687%. <- this value is our variance which admittedly isn’t very useful in this form.
Step 5: Turning the variance into the standard deviation, a useable form for interpretation.
(.687%)^1/2= 8.29%. <- the interpretation is that this stock has a variation of 8.29% from its mean.
Standard Deviation in Excel
While calculating the standard deviation by hand may be useful to get an understanding of the mechanics of the formula, it is not realistic to do so in practice. Instead, we can use a prebuilt function in excel to automate the calculation for us and reduce the risk of human error.
To perform the calculation for standard deviation for a sample we can use the “=STDEV.S” function in excel. If we were to apply this function to the same scenario we used above the result would be the same “8.29%”.
Frequently Asked Questions
A good standard deviation for a stock is 6% or less which would indicate the stock’s price is relatively low in volatility and possibly more predictable.
Find the standard deviation for a stock as follows:
- Calculate the average of the returns over the number of time periods.
- Subtract each return from the average return then square that value.
- Sum the squared values from above and divide by the count of the values minus 1.
- Finally, take the square root of this value. This is the standard deviation.
- Substitute price if looking for price deviation instead of % return deviation.
A low standard deviation is better as it means the data is more clustered around the average. Since the data is cluster more closely around the average is more representative of the individual values in the data set.