The Practical way to Calculate Yield to Maturity
In short:
If you invest in bond’s odds are you’ll hear about yield to maturity. Likely you’ll also hear a bond’s yield to maturity and its price are intricately linked. So, what exactly is yield to maturity, how is it connected to the price of a bond, and how is it calculated?
Yield to Maturity (YTM) is the expected rate of return on a bond or fixed-rate security that is held to maturity. Since bonds do not always trade at face value, YTM gives investors a method to calculate the yield (or rate of return) they can expect to earn on a bond.
Investors will calculate the YTM by discounting all future payments and the repayment of the face value back to what their present value is. In other words, what would the sum of all those payments be worth if they were received today. This value will be the current price of the bond when discounting by the correct YTM -i.e. this is how YTM and current price are linked.
Key Points
- Yield to Maturity is the expected return of a bond held until maturity.
- Current Price and YTM are directly connected to each other.
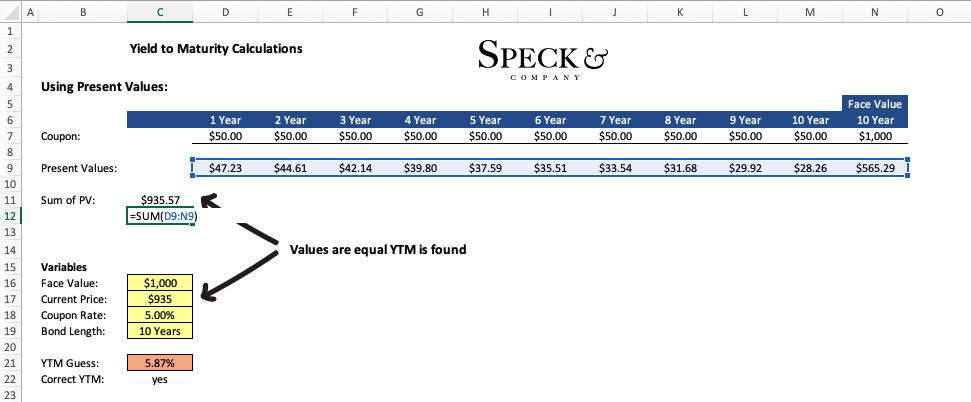
- YTM is found when the Present Value of all future cash payments equals the current price of the bond.
How Bonds are Priced
When looking at a bond and trying to figure its yield to maturity, you will have a few variables that you will know. These will include the years left until maturity, the number of times payments are made a year (annual, semiannual, etc.), the actual payment amounts (cash figure or you can calculate the cash figure), the current price of the bond, and the face value.
With those known variables you can calculate the yield to maturity by inserting different values for the “Rate” variable in the formula above. You will know you have the correct rate for YTM when the sum of all values on the right is equal to the “Bond Price”.
Calculating Yield to Maturity In Excel – Hard Way & Easy Way
Here’s an example that we’ve set up in excel.
Say we are looking at a bond that is currently trading at $935, has 10 years left until mature, the face value of the bond is $1,000, and pays an annual coupon of $50 -i.e. paid once per year. What is the YTM for this bond?
From this point, we have multiple ways we can find the YTM in excel. Here is one approach which is a little involved but shows how the mechanics of the formula above is working.
You can download this file for free here:
Final Result
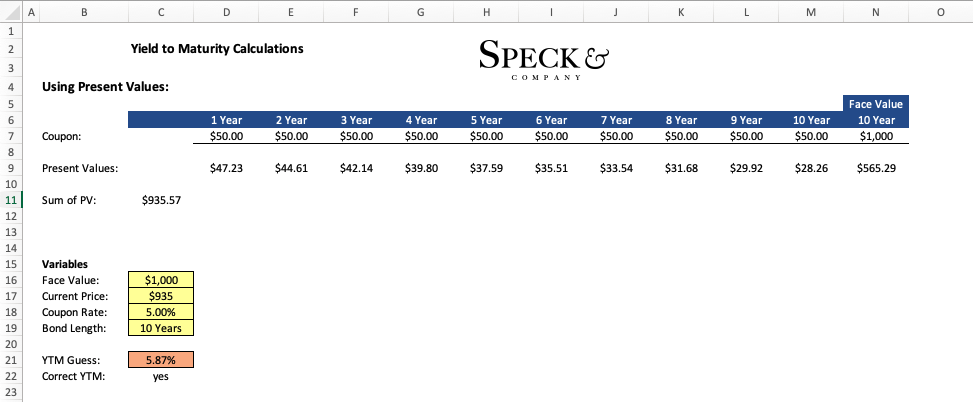
Step 1 – Discounting the payments
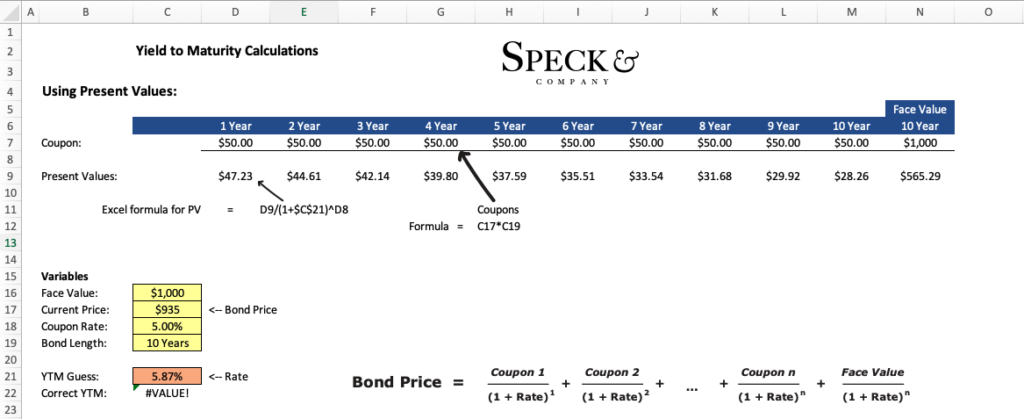
Step 2 – Sum the discounted values
Calculating Yield to Maturity in Excel – Quick Approach
While the approach we used above is great for an illustrative purpose, likely you will not want to build out a spreadsheet every time you need to calculate the YTM of a bond. Instead, excel has already built-in functions that will calculate this value for us if we insert the values in the right spots.
To calculate YTM in excel with a prebuilt function, simply find a cell in excel and type “=RATE”.
We can use the same values from the above example to see how it would work.
The important thing to note is that the current price should be entered as a negative value, and the periods are not necessarily the number of years. For example, if you have a semi-annual payment you would want to take the coupon value and divide it by 2 since you are getting half the coupon in the beginning of the year and half in the end of the year (timing difference –> time value of money).
Applying this to our example, if we had semiannual payments our coupon would be $25 ($50/2) and our periods would be 20 (10*2).
This would have a major impact on the value we get for YTM so make sure you make note of this.
Yield to Maturity in Excel Underlying ideas
What’s going on behind the scene during the calculation?
Truly understanding yield to maturity requires an understanding of a few foundational components of finance. If you can get a sense of these concepts then understanding what is going on with YTM should be more intuitive.
Time Value of Money – what’s happening during the calculation
The time value of money is actually a really simple concept, all it means is that money today is worth more than money tomorrow. But how can this be? Isn’t $1 today still $1 tomorrow? Yes, however, time has passed meaning you could have done something with that money over that one day to earn more money. The simplest thing is an interest-bearing savings account.
Time value of money applies to bonds in that the same coupon an investor receives 15 years after they purchase the bond will be less valuable than the same coupon they are receiving today. Yield to maturity gives investors a way to account for this.
Present Value – what’s happening during the calculation
So how do you account for the time value of money issue on bonds? You calculate out what all the coupon’s value would be if they were all received today, called the present value. The fancy way to say this is that you discount future coupon values back to their present value -which is what YTM is doing.
We can take all the present values and set them equal to the current price of the bond to find equilibrium. When we achieve both sides being the same value we have found the discount/interest rate.
Frequently Asked Questions
Yield to Maturity (YTM) is the expected rate of return on a bond or fixed-rate security that is held to maturity. There are two formulas to calculate yield to maturity depending on the bond. The yield to maturity formula for a zero-coupon bond: Yield to maturity = [(Face Value / Current Value)(1 / time periods)] -1. The yield to maturity formula for a coupon bond: Bond Price = [ Coupon x (1 – (1 / (1 + YTM)n) / YTM) ] + [ Face Value x (1 / (1 + YTM)n ) ]
Yield to maturity can be calculated in excel with the rate function. To calculate the yield to maturity you will need the current price, the face value, the years periods until maturity, and the coupon payment per period. With those variables, you can type “=RATE” into excel and enter the values as follows RATE(periods, coupon, -current price, face value).
The current yield formula is the bond’s annual coupon divided by its current price. This value reflects the percentage return an investor would receive from buying the bond at the current price and holding the bond for one year.